ANÁLISE DO INVESTIMENTO EM OURO – 2

 

Este post é o segundo de uma série de três artigo que elaborei sobre o investimento em ouro no Brasil. Para visualizar os outros artigos, acesse:

 

http://www.contratofuturo.com/artigos/

 

Artigo 1: Evidências Históricas da Performance do Mental

Artigo 2: Benefício da Diversificação de Carteira com Ouo

Artigo 3: Fatores que Influenciam o Investimento em Ouro no Brasil

 

 

BENEFÍCIO DA DIVERSIFICAÇÃO DE CARTEIRA COM OURO

 

No intuito de avaliar o investimento em ouro no Brasil, o presente artigo busca avaliar, através de backtests, a comprovação de que, agregar o metal a portfólios em mandatos restritos de renda fixa e renda variável, promove uma melhora significativa nos retornos em relação aos benchmarks. Com isso, os principais argumentos em favor do metal poderiam ser comprovados e validariam as implicações positivas de investir em ouro. Mas primeiro, vamos rever alguns conceitos de diversificação: 

 

1 – A MODERNA TEORIA DE CARTEIRAS

 

A Moderna Teoria de Carteira (Modern Portfolio Theory – MPT) e o conceito de diversificação e risco de um portfólio, são atribuídos em grande parte a Harry Markowitz. Formando em matemática, divulgou o seu trabalho em um artigo no Journal of Finance em 1952 e a essência de seus estudos é encontrada na obraPortfolio Selection, 1959. As formulações para cálculo do risco de um portfólio são provenientes do modelo desenvolvido por Markowitz, a quem foi atribuído o Prêmio Nobel de Economia em 1990. (ELTON 2012)

“Tendo em vista que, em portfólio, os ativos correlacionam-se de maneiras distintas, de acordo com sua alocação, é preferível que um investidor opte por um portfólio diversificado que não esteja exposto a um único fator de risco correlacionado”. (ASSAF NETO, 2013 pag. 229).

Influenciado por premissas desenvolvidas por Irving Fisher (1906); von Neumann e Morgenstern (1944); e John B. Williams (1938), o matemático americano propôs uma abordagem baseada na teoria dos jogos, onde calcula-se estimativas de retorno (expectativa), risco (variância) e correlação entre as variáveis aleatórias. Estes são os pontos básicos para a fórmula matemática da diversificação de carteira, ou seja, o grau de risco de uma carteira tem a ver não só com os ativos específicos que a compõem, mas também com a correlação em que eles oscilam analogamente. Markowitz (1959) definiu um portfólio “eficiente”, capaz de dar o máximo retorno esperado potencial a um determinado grau de risco.

O processo de estruturação de um portfólio eficiente, segundo Assaf Neto (2013), consiste na análise da alocação de ativos:

 

1.1. Alocação de Ativos

A teoria dos portfolios trata essencialmente da composição de uma carteira ótima de ativos, tendo por objetivo principal maximizar a utilidade (grau de satisfação) do investidor pela relação risco/retorno .

O retorno esperado de uma carteira composta por mais de um ativo é definido, segundo Elton (2012), pela média ponderada do retorno de cada ativo em relação a sua participação total na carteira. Logo, o retorno esperado ponderado da carteira pode ser obtido pela seguinte expressão de cálculo:

          

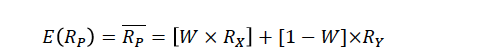
onde:   E(R) = retorno esperado ponderado da carteira;

W = percentual da carteira aplicado na ação X;

(1-W) = percentual da carteira aplicado na ação Y;

R (x e y) = retorno esperado das ações X e Y, respectivamente.

 

Logo, dado o retorno esperado de cada ativo de uma carteira, o retorno esperado de toda carteira depende da proporção investida em cada ativo que a compõem.

Para uma carteira constituída por n ativos, o retorno esperado é obtido pela seguinte expressão:

onde: W(j) representa a proporção do capital total investido no ativo j; n, o número total de ativos que compõem a carteira e R(j), o retorno esperado do ativo j.

 

Um aspecto relevante do portfólio, segundo Brito (2006), é que o risco de um ativo mantido fora de uma carteira é diferente de seu risco quando incluído na carteira. No estudo da diversificação, o risco de um ativo é avaliado por sua contribuição ao risco total de uma carteira. Elevando de uma maneira diversificada o número de títulos de uma carteira, é possível promover-se a redução do seu risco, porém a uma taxa decrescente. A partir de determinado número de títulos, a redução do risco praticamente não ocorre mais, e a carteira conserva, de forma sistemática, certo nível de risco.

O risco de uma carteira depende não somente do risco de cada elemento que a compõe e de sua participação no investimento total, mas também na forma como seus componentes se relacionam (covariam) entre si. Ainda com o que foi comentado no tópico anterior, relacionando-se ativos com baixa correlação (ou covariância inversa), é possível reduzir-se o risco total de uma carteira. (BODIE, KANE e MARCUS 2010)

Nessas condições, o risco de uma carteira constituída de dois ativos (X e Y) pode ser obtido com base nas seguintes expressões:

 

Observa-se que o desvio-padrão de um portfólio de dois ativos não é obtido unicamente pela soma do desvio-padrão de cada ativo ou até mesmo por sua média aritmética ponderada. A expressão de cálculo considera também a covariância entre os ativos a expressar a contribuição de diversificação sobre o risco do portfólio.

Assim, a redução do risco de uma carteira pode ser promovida pela seleção de ativos que mantenham alguma relação inversa entre si. Ressaltando colocações anteriores, o objetivo da diversificação é o de combinar ativos de forma que reduza o risco do portfólio.

A expressão geral de cálculo do risco (desvio-padrão) de uma carteira que contém “n” ativos, baseando-se no modelo desenvolvido por Markowitz, é:

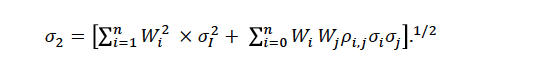
Visando demonstra os benefícios da diversificação segundo a Moderna Teoria de Carteira, apresenta-se dois dos indicadores estudados: Ouro e Ibovespa, dados de risco e retorno anual. Segundo Markowitz (1959), o risco de dois ativos combinados em uma carteira e que possuem correlação menor que 1, sempre será menor que a media pondera dos riscos dos ativos de investidos de forma separada.

 

Gráfico – Relação Risco e Retorno – Ibovespa, Ouro e carteira com 50% dos ativos.

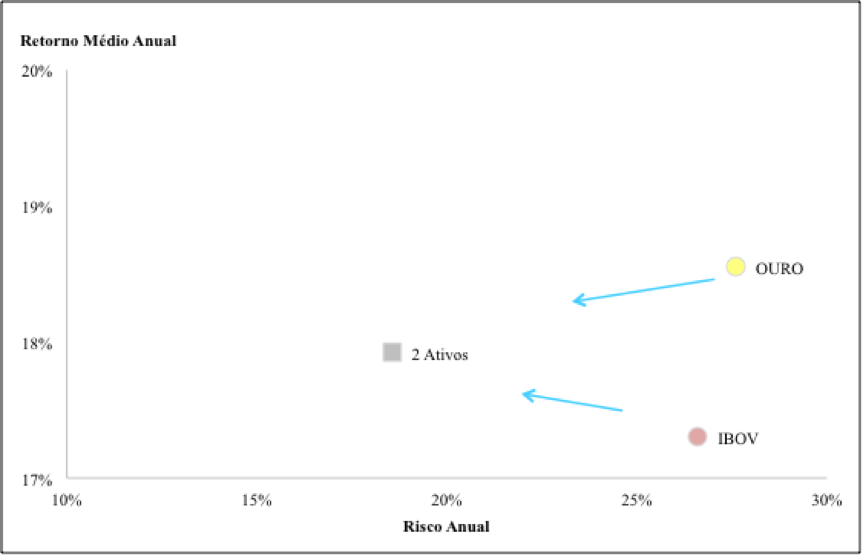
Fonte: Elaboração do autor

 

A diversificação, conforme proposta por Markowitz, permite a redução ou até eliminação total do risco diversificável (não sistemático) de um portfólio. Porém, será sempre presente a parcela do risco sistemático. Os efeitos da diversificação sobre o risco de uma carteira costumam ser relevantes na maioria dos estudos de finanças. (ELTON 2012)

Nesta ampla abrangência do entendimento do risco, pode se introduzir que o risco total de qualquer ativo é definido por sua parte sistêmica (risco sistemático ou conjuntural) e não-sistemática (risco específico ou do próprio ativo). Fórmula:

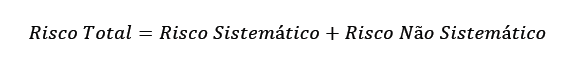
Utilizando os mesmos ativos para formar uma carteira – Índice Ibovespa e Ouro – apresenta-se os seguintes resultados, separados (dados mensais):

Tabela – Retorno e Risco de Ouro e Ibovespa mensal

Fonte: Elaboração do autor

O índice da bolsa de valores brasileira apresentou, entre o período de 1999 a 2014, o retorno mensal de 1,43%, como um risco de 7,76%. Já o ouro obteve 1,46% de retorno com uma volatilidade de 8,19%. A covariância entre os ativos é de -0,2%.

A tabela abaixo ilustra o risco e retorno dos ativos estudados assumindo diferentes proporções no portfólio. Observa-se que a redução do risco do portfólio somente se processa quando eles são colocados juntos, diversificando a carteira, e não quando analisados separados (média ponderada), beneficio da correlação negativa.

Tabela – Carteiras mistas entre Ibovespa e Ouro – Risco ponderado e segundo Markowitz

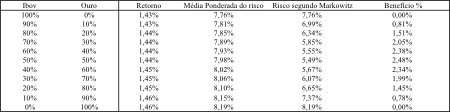
Fonte: Elaboração do autor

 

Se o índice de correlação entre os ativos é menor que1,00 ( = -0,3319), promove-se, pelo modelo de diversificação, o beneficio da redução do risco do portfólio. O desvio-padrão do portfólio, apurado pela formulação de Markowitz (1959), é sempre inferior ou igual para qualquer participação dos ativos no total do investimento, à media ponderada do desvio-padrão dos retornos dos ativos. Em evidencia, o maior benefício ocorre na situação de correlação negativa dos retornos.

Ao se aplicar as possíveis combinações de carteiras entre os ativos Ibovespa e Ouro, pode-se obter os resultados relativos a cada composição, conforme tabela anterior. Os diversos resultados relatados descrevem uma curva que retrata o conjunto possível de combinações de carteiras, conforme ilustrado no gráfico abaixo:

Gráfico – Fronteira Eficiente – Relação de carteiras entre Ouro e Ibovespa

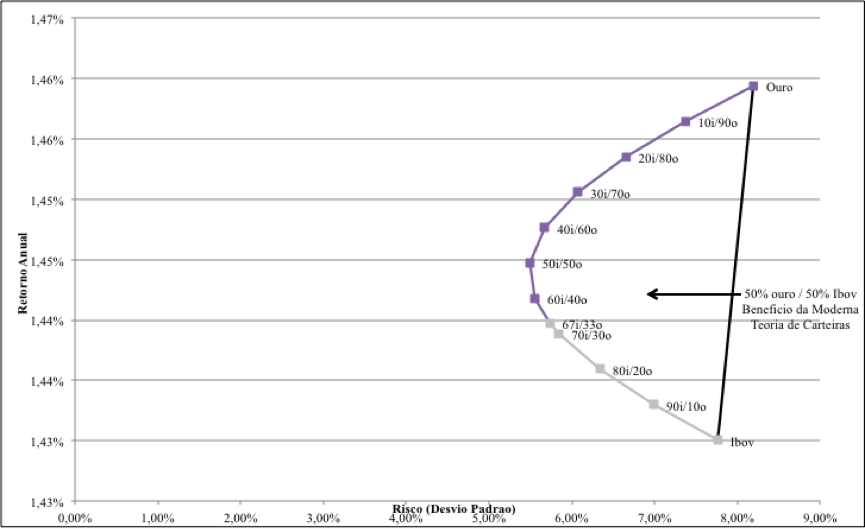
Fonte: Elaboração do autor

 

A curva destacada a esquerda – que representa diferentes combinações entre uma carteira composta por x% de Índice Bovespa e x% de Ouro – evidencia o efeito da diversificação de carteira pela redução de risco. Chamada de Linha de Alocação de Capital (LAC), esta curva convexa demonstra que ativos que não apresentem correlação perfeitamente positiva (< 1,0) promovem, em consequência, redução de risco da carteira. (ELTON 2012)

Também no gráfico, pode-se visualizar uma reta entre os ativos Ibovespa e ouro, que reflete os possíveis resultados que os ativos apresentariam se fosse apurados separadamente, ou com uma correlação perfeitamente positivas (= + 1,0), ou a média sem o beneficio da diversificação pela Moderna Teoria de Carteiras.

A seleção da carteira de investimento mais atraente para um investidor racional, segundo Assaf Neto (2013), que avalia a relação risco/retorno em sua decisão, restringe a escolha para as carteiras que estão acima do ponto de inflexão da curva convexa da Linha de Alocação de Capital, como pode-se notar no gráfico.

Chamada de Fronteira Eficiente (FE), a partir do ponto de inflexão há a Carteira de Variância Mínima (CVM) e acima desta todas as carteiras que possuem maior risco e maior retorno. O ponto que tangenciam a FE e a LAC é a maximização da relação risco e retorno, obtendo-se as carteiras ótimas de ativos com risco. As alternativas de investimento que atendem a essa orientação são aquelas dispostas na parte superior da curva convexa – denominadas por Markowitz (1959) deeficientes.

 

Gráfico – Fronteira Eficiente – Maximização da relação de carteiras entre Ouro e Ibovespa

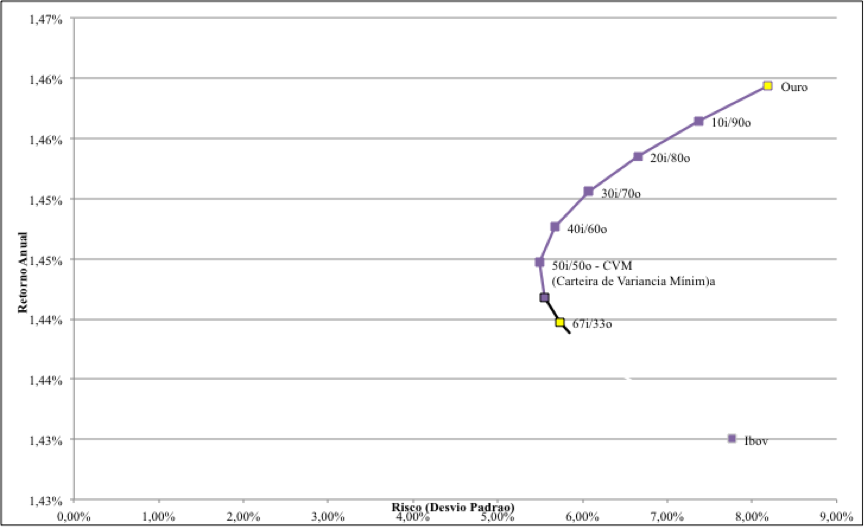
Fonte: Elaboração do autor

 

Em outras palavras, na Fronteira Eficiente, é possível selecionar uma carteira que apresenta, para determinado risco o melhor retorno possível. E, mesmo que o investidor deseje um baixo risco/retorno, ele pode maximizar este retorno com o mesmo nível de risco. Mendonça (2011) também ressalta existe inúmeros tipos desoftwares disponíveis e que podem ser aplicados no estudo de seleção de carteiras.

 

1.1.2 Alocação de Capital

Conhecendo o portfólio máximo de risco de risco, o investidor passará por um último processo de decisão, em que o investidor, de acordo com suas premissas de aversão a risco decidirá quanto será alocado no portfólio de risco e no ativo livre de risco. Ao final o investidor terá uma carteira global formada por n% no portfólio ótimo com risco e de n% no ativo livre de risco. Como apresentando no gráfico da fronteira eficiente dado um conjunto de ativos, existirá um portfólio ótimo dado o nível de aversão ao risco. Desta forma, mesmo tendo os mesmo ativos em carteira o retorno e o risco corrido pelos investidores serão diferentes, necessitando de mais ou menos ativos de baixo risco. (BODIE, KANE e MARCUS 2010)

A moderna teoria de carteira é um dos pilares da teoria de finanças. Com este conceito os investidores podem determinar uma carteira ótima e um conjunto de possibilidade de alocação, a partir de uma análise e seleção de ativos. Entretanto, o modelo apresenta falhas sob certos aspectos práticos. A volatilidade do ativos, que alterada diariamente, fará com que a matriz de covariância seja alterada também, levando ao investidor alterações excessivas no portfólio, o que implicaria em custos demasiados (o modelo não faz menção a custos por operação). Outro problema é que Markowitz (1959) considera apenas os efeitos da diversificação entre ativos de risco. Quando introduzido ativos como CDI, que são considerados “livres de risco”, o modelo apresenta pouca melhora nos resultados.

Visando aprimorar os modelos financeiros, alocando também ativos de renda fixa nas carteiras, maximiza-se as opções disponíveis para o investidor. Quando introduzido um ativo sem risco, a fronteira eficiente assume a forma de uma reta, ligando a o ativo livre de risco com a tangente da fronteira eficiente dos ativos com risco. Este ponto de tangência é chamado de “Optimal Portfólio“. Esta é a base para o desenvolvimento do Capital AssetPrice Management (CAPM), proposto por Bill Sharpe e outros pesquisadores.

 

1.2 MODELO DE PRECIFICAÇÃO DE ATIVO

 

Baseado na Moderna Teoria de Carteiras de Markowitz (1959), o modelo de precificação de ativos CAPM Capital Asset Price Model apresenta métricas para mensurar os componentes da avaliação entre risco e retorno, incluindo também ativos livres de risco. Entre os resultados, o modelo visa maximizar a expectativa de retorno esperado para determinado nível assumido de risco, além de calcular a taxa de retorno teórica requerida em consideração a sensibilidade do ativo ao risco sistêmico.

Amplamente difundido no campo das finanças, Hull (2010) observa que a teoria é o conjunto de artigos escritos por Sharpe (1964), Lintner (1965), Mossin (1966), posteriormente incluídos Tobin (1958), Treynor (1962) e Jensen (1972).

A tese do CAPM possui algumas falhas em suas suposições, trazendo alguns questionamentos com relação a sua eficácia. Outros modelos como o APT (Arbitrage Pricing Theory), o Re-balanceamento Eficiente de Michaud (2008) e os modelos multifatoriais visão melhorar suas falhas, porém, devido aos méritos e ampla aceitação entre os investidores do mercado, a hipótese da precificação de ativos CAPM é a mais difundida no meio acadêmico. (ASSAF NETO 2013)

 

1.2.1 CAPM

 

Primeiro a expandir o trabalho de Markowitz, James Tobin (1958) utilizou estudos econométricos para investigar as relações de variáveis endógenas (Modelo de de Tobin) com o mercado, introduzindo o chamado ativo livre de risco a teoria. Ao analisar a relação entre risco e retorno entre classes de ativos, o autor descreve a reta conhecida por Reta do Mercado de Capitais (CML – Capital Market Line).

A inclinação da reta indica a remuneração (prêmio) exigida pelo mercado para cada unidade de risco. Os ativos inferiores (e também menor retorno) são os títulos de emissão pública, sendo alguns entendidos pelo mercado como livres de risco (Risk free). Esses títulos indicam a origem da reta do mercado de capitais. Segundo Póvoa (2010), CDI e Índice Bovespa são os benchmarks mais utilizados no Brasil com relação a renda fixa e variável.

Onde: = Renda fixa, = retorno de mercado (variável), = desvio padrão do mercado e = desvio padrão do portfólio/carteira.

 

Outro expoentes do campo das finanças, William Sharpe (1964), é a principal referencia na formalização do modelo de precificação de ativos – CAPM. Seu estudo complementou a MPT com a adição do conceito Beta e risco sistêmico, além do estudo de performance dos ativos.

O Índice Beta é um indicador que mede a sensibilidade de um ativo em relação ao comportamento de uma carteira que represente o mercado. É, por exemplo, a relação entre a variação do retorno de uma ação (ativo) e o Ibovespa (mercado), como descrito por Póvoa (2010). A relação entre o retorno esperado e o beta é linear, isto é, a linha reta é denominada Reta Característica do Ativo (beta é a medida de inclinação – regressão linear dos ativos).

Portanto, o coeficiente Beta é uma medida do risco que um investidor está exposto ao investir em um ativo em particular em comparação com o mercado como um todo ou risco sistemático.

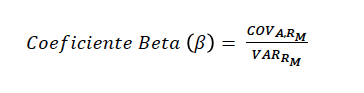
Mendonça (2011) destaca que, além da contribuição de Sharpe (1964) para a teoria de carteira ao apresentar coeficiente beta como parâmetro para risco sistêmico, o índice de Sharpe é um dos indicadores mais utilizados pelo mercado financeiro para medir a performance dos fundos de investimentos.

O indicador proposto de Sharpe (1964) é definido como a razão entre o prêmio de risco (retorno esperado – retorno do ativo livre de risco) e a volatilidade do investimento. A fórmula do índice de Sharpe ex-ante é:

Para fazer o cálculo ex-post do índice de Sharpe, ou seja, utilizando valores realizados, é preciso primeiramente calcular o retorno médio do investimento e da taxa livre de risco, assim como a volatilidade.

A razão de Sharpe possui a seguinte interpretação para Mendonça (2011): “Ele representa o retorno em excesso ou prêmio de risco (isto é, acima da taxa livre de risco) por unidade de desvio padrão do retorno.” Logo, quanto maior for o índice de Sharpe, melhor o resultado com relação ao mercado.

É importante ressaltar que o indicador apresentado pelo modelo CAPM de Sharpe (1964) possui certas fragilidades, relacionadas ao fato de que a medida de risco utilizada é a volatilidade . Isto implica no fato que o índice de Sharpe, por si só, não é útil para avaliar investimentos que possuem distribuições de retorno assimétricas, ou com a existência de valores extremos. Elton (2012) destaca que séries de retornos de ações são, em sua maioria, assimétricas e com caudas longas negativas. Encontram-se versões generalizadas do índice de Sharpe que levam em considerações esta assimetria da distribuição e a existência de valores extremos.

Após a elaboração de diversos indicadores para avaliar a relação entre risco e retorno de ativos ou de uma carteira, o modelo CAPM constata que alguns resultados demonstram desempenho acima de seu benchmark proposto. O parâmetro do modelo conhecido como Alfa (α) de Jensen (1972), é o coeficiente apresentado pelo autor para expressar o relação de prêmio de risco oferecido pelo ativo (ou carteira), na hipótese de excesso de retorno em relação ao mercado. Em outras palavras, é o indicador que mede o desvio da performance superior do portfólio daquela prevista pelo CAPM.

Damodaran (1997) calcula o excesso de retorno do CAPM através da equação:

 

Na avaliação de Van Horne (1998), o valor de alfa de uma ação deve ser inicialmente zero. Se a inclinação da reta de alfa é negativa ou menor que o CAPM, o investidor racional irá preferir o melhor resultado esperado proveniente de combinações de ativo sem risco. Caso seja maior, irá preferir os ativos de maior alfa.

Por fim, devemos classificar os fundos no Brasil, para poder analisar quais formas podemos aplicar ouro no portfolio.

 

1.3 FUNDOS DE INVESTIMENTO NO BRASIL

Ao alocar seu capital em um fundos de investimentos, o investidor brasileiro depara-se com uma ampla gama de opções, as quais propõem-se a replicar ou superar o benchmark estabelecido. Chamado de mandato passivo ou ativo, as formas de investir do gestor são classificadas de acordo com os ativos em que ele aloca os recursos. O órgão regulador dos fundos de investimento no Brasil é a Anbima (Associação Brasileira das Entidades dos Mercados Financeiro e de Capitais).

Para facilitar o processo de decisão de investimento a Anbima atualiza constantemente a classificação dos fundos de investimento. As alterações visam contribuir aumentando a transparência no mercado, permitindo a adequada comparação entre os fundos. A segregação é estabelecida com relação aos benchmarksexistentes no mercado, à exemplo dos padrões internacionais, o que preserva também as características da indústria local.

A orientação do órgão se dá em três diferentes níveis: regulação, onde analisa-se a classe de ativos, e a auto-regulação, separada em tipo de gestão (risco) e estratégia. A CVM considera que o primeiro nível obedece à classificação definida na Instrução nº555/14 da CVM, que regula a indústria de fundos. Isto é, conta com as classes renda fixa, multimercados, ações e cambial (ANBIMA[1]).

As segregações subsequentes são instituídas pela Anbima. O segundo e terceiro nível são padronizados pela instituição para fins de comparação e auxilio ao investidor. O organograma detalhado é apresentado logo abaixo:

Figura – Organograma, classificação de fundos de investimento – Anbima

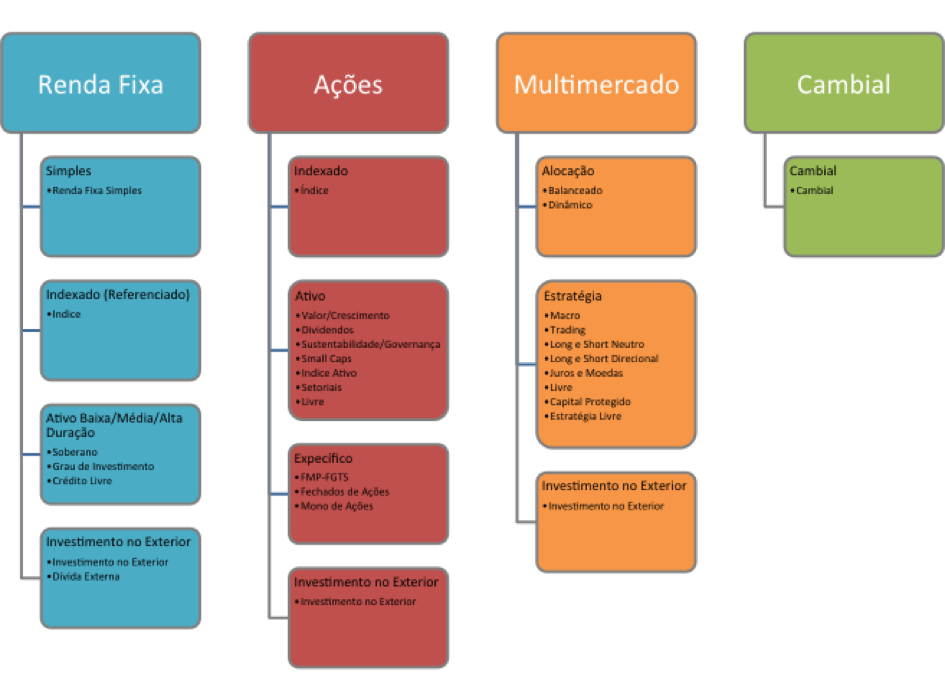
Fonte: Anbima – Elaboração do Autor

Este estudo irá atentar-se sobre os fundos geridos através de mandatos referenciados. Avaliando os desempenhos, a fim de averiguar se a adição de ouro (OZ1D) aos portfólios agrega benefícios, implicando em carteiras mais eficiente.

Para tal estudo, a seleção de fundos de investimento atrelados ao benchmark será: Renda Fixa Simples, onde, no mínimo, 80% dos ativos são indexados ao CDI; Renda Fixa Indexado, com mínimo de 95% dos ativos indexados ao CDI; Ações Livre, devem possuir no mínimo, 67% da carteira em ações à vista e outras formas de investimento em renda variável; e Ações Indexado, onde 95% da carteira deve replicar a composição do índice Bovespa vigente no período[2]. Não será avaliado fundos multimercados e cambiais, devido a seus mandatos mais amplos e breve benchmark histórico.

 

 

2         Resultados do OURO em fundos de investimento

 

Estudando o investimento em ouro no mercado financeiro no artigo anterior e realizando backtest em portfólios reais, pretendo encontrar os resultados e compará-los ao benchmark de cada uma das seleções.

Nos resultados anteriores, vimos que para a teoria financeira MPT de Markowitz (1959) as inter-relações entre os ativos não precisão ser necessariamente significantes, mas sim seja pouco correlacionadas. Os resultados encontrados anteriormente são de correlação positiva entre ouro e o dólar americano, negativa em relação ao mercado de ações e inflação, e pouco correlacionado com o mercado de renda fixa. Nenhum dos benchmarks é próximo a 100% de correlação com acommodity e todos devem demonstrar-se como alternativos para diversificação de um portfólio. Para esta avaliação, o modelo CAPM promove maior embasamento empírico.

 

2.1 Análise do CAPM

 

A modelagem de CAPM proposta por Sharpe (1964) deixa um grande legado para avaliação de ativos, embasando diversas obras posteriormente escrita. Seu objetivo é demonstrar as relações e contribuições marginais da diversificação de ativos em comparação com o benchmark proposto.

Este grupo de indicadores calculados não apresentam estimadores econométricos, retornando relações lineares entre o retornos dos ativos e seus benchmarks. Sua mensuração ocorre de modo ex-ante, comparando diferentes ativos financeiros, no intuito de buscar aqueles que apresentam melhor benefício agregado.

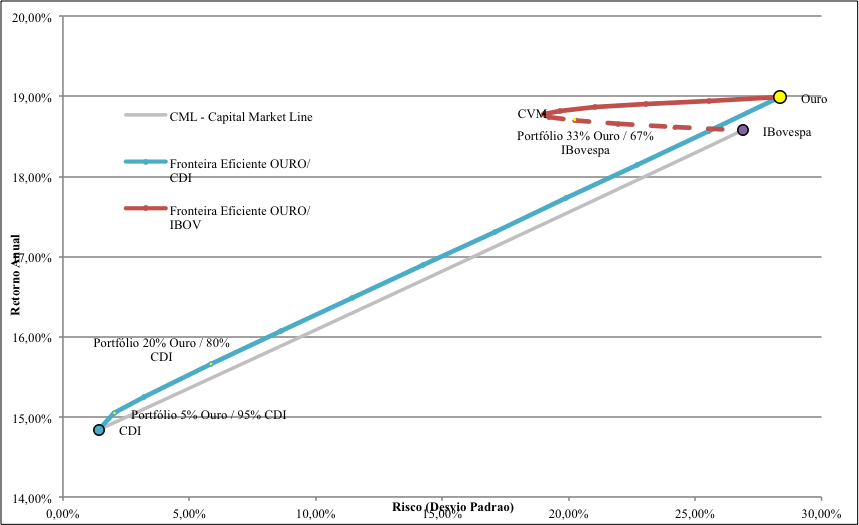
Foi mensurada a relação de risco e retorno do ouro e os dois principais benchmarks de mercado de mercado, renda fixa CDI e renda variável Ibovespa. O gráfico abaixo apresenta a CML, referente ao prêmio de risco do mercado financeiro, junto as Fronteiras Eficientes de portfolios diversificados entre ouro/CDI e ouroIbovespa.

Gráfico – Fronteiras Eficientes, mesclando carteiras OZ1D, dólar e Ibovespa.

Fonte: Elaboração do autor

 

As primeiras interpretações acerca dos gráficos sugerem que a diversificação ouro/CDI versos a relação linear de prêmio de risco de mercado (CML) é mais benéfica ao investidor. Dentre o conjunto de carteiras, ponderado pelo risco , qualquer portfólio apresenta alfa superior a média ponderada dos ativos, benefício mais perceptível na inclinação do inicio da diversificação.

Com relação as proxys de renda variável e as carteira ouro/IBov, a diminuição de risco é mais visível do que comparada com ativos livres de risco. Para Elton (2010), a partir da Carteira de Variância Mínima (CVM) que no gráfico é de 51% em Ouro e 49% Ibovespa, a Fronteira Eficiente começa e sugere que a alocação superior em ouro que promove melhores retornos, novamente ponderados pelo risco que o investidor deseja. Porém, segundo regra da ANBIMA, a carteira de diversificação máxima permitida em mandatos de fundos de investimento classificados como renda variável é de 67% Ibovespa e 33% outros ativos. Utilizando ouro os percentuais máximo permitido de outros ativos em ouro, a limitação resulta em um carteira que encontra-se abaixo da FE do ativos sugerida pela teoria financeira, porém, mesmo assim, há evidências de que a diversificação diminuiu o risco dos ativos e melhorou a rentabilidade do benchmark Ibovespa. Veremos isso no próximo tópico:

 

2.2 RESULTADO AO AGREGAR OURO A FUNDOS DE INVESTIMENTO

 

Descreve-se a seguir o processo de simulação (backtest) visando medir os resultados de agregar ouro à portfólios de fundos de investimento. Analisa-se se há o beneficio da diversificação sugerido por Markowitz (1959) e quais os resultados segundo o modelo CAPM de Sharpe (1964). Com balanceamento fixo, conforme regras ANBIMA apresentadas no capitulo anterior, não houve otimização de carteira durante as operações. Inicialmente calculou-se a alocação de carteira em RF, conforme os mandatos referenciado (95% em CDI) e renda fixa puro (80%).

Graficamente é apresentado a evolução de preços do ouro, CDI e as carteiras de RF alocando 5% e 20% em ouro.

 

Gráfico – gráfico OZ1D, CDI e carteiras mescladas ouro + CDI

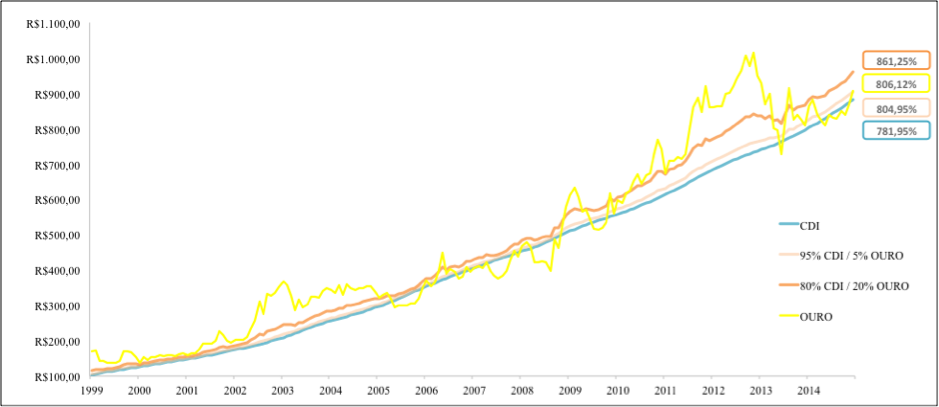
Fonte: Elaboração do autor

 

Tabela – Estatísticas OZ1D, CDI e carteiras mescladas ouro + CDI

Fonte: Elaboração do autor

Ao agregar o metal em 5% e 20%, o retorno das carteiras apresentou melhora no retorno anual resultando em 102,94% e 106,99% do CDI. A volatilidade neste mesmos mandatos aumentou para 2,00% e 5,72% ao ano. A elevado do ouro aumentou os riscos das carteiras e os benefícios da diversificação não são tão evidentes neste backtest. Uma alocação de 5% pode ser sugerida para investidores que aplicam em renda fixa, dado que o retorno continua 100% positivo ao longo do tempo o VAR e teste de stress estimados não apresentam resultados esperados negativo. Uma alocação maior, de até 20% pode melhorar os resultados, porém cabe ao investidor saber seu nível de aversão a perda e confrontar com os resultados apresentados.

O segundo backtest foi aplicado ao mercado de renda variável, agregando ouro a fundos de investimento indexados ao Ibovespa conforme regra ANBIMA. Utilizando o benchmark como proxy de retorno em 67% da alocação, os outros 33% foram aplicados no metal. Os resultados encontram-se no gráfico e tabela abaixo:

 

Gráfico – Gráfico OZ1D, Ibovespa e carteira mesclada 67% Ibovespa – 33% OZ1D

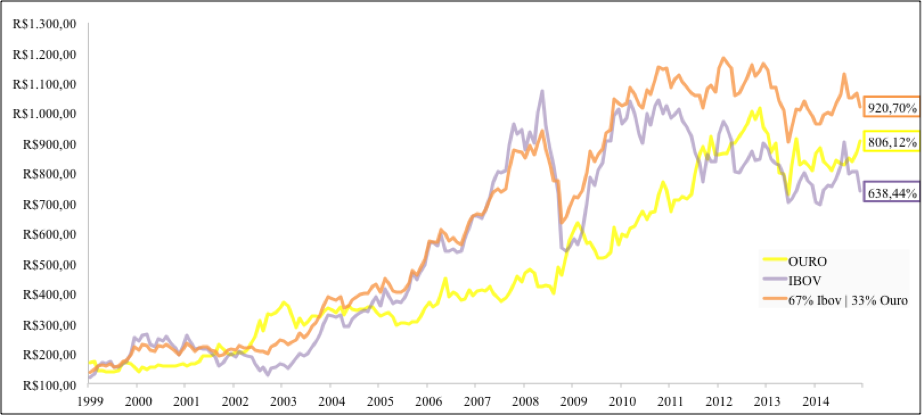
Fonte: Elaboração do autor

 

Tabela – Estatísticas OZ1D, Ibovespa e carteira mesclada 67% Ibovespa – 33% OZ1D

Fonte: Elaboração do autor

 

Os resultados evidenciam melhor o benefício proposto por Markowitz (1959) da diversificação. Apesar da carteira encontra-se abaixo da Fronteira Eficiente sugerida pelo modelo, o benefício da menor volatilidade promoveu também um retorno superior acumulado.

O retorno total do portfolio de 920,70% é superior ao investimento em 144,21% ao benchmark. O risco decaiu para 19,5%, a volatilidade downside é de 10,09% e no simulado 56,25% dos meses foram positivos. Por fim, os parâmetros de risco máximo estimados encontram-se no VaR -5,42% com 90% de significância, -6,35% com 95% e -10,13% com 99% de significância, além do teste de stress em -31,04%, resultado muito menor que os dois ativos analisados separadamente.

O beta em 0,65 demonstra menor sensibilidade da carteira ao risco de mercado, e alfa de 0,09%. O índice de Sharpe apresentou resultado de 0,16, superior ao ouro em 0,14, assim como índice de Treynor em 0,05, porém o índice de Sortino ficou aquém do resultado do metal. Por último, a relação risco/retorno apresenta melhora na carteira diversificada, conforme gráfico:

 

Gráfico – Relação risco/retorno OZ1D, Ibovespa e carteira 67% Ibovespa – 33% OZ1D

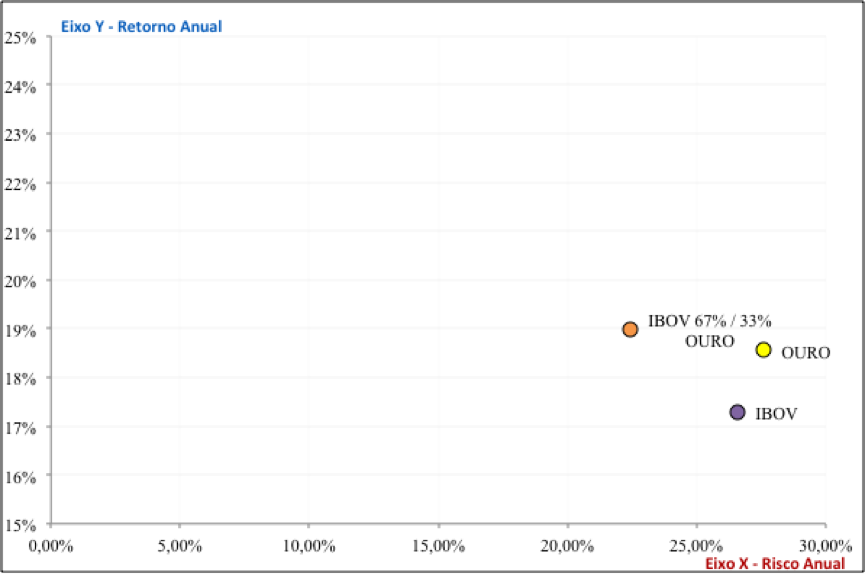
Fonte: Elaboração do autor

 

Pode-se concluir que as carteiras que possuíram ouro em sua alocação apresentaram retornos consistentes ao longo da série, e, conforme MPT, a diversificação de ativos pouco correlacionados promoveu a redução de risco, principalmente em comparação a ativos voláteis. O arcabouço da teoria financeira comprova que oinvestir na commodity no Brasil resulta em agregação de performance aos portfólios.

 

 

 

3         CONCLUSÃO

 

Para concluir, foram simulados os resultados de agregar ouro à portfólios de fundos de investimento conforme regra da ANBIMA. Ao adicionar o metal em 5% e 20%, o retorno das carteiras de renda fixa apresentaram melhora no retorno anual resultando em 102,94% e 106,99% do CDI. A volatilidade neste mesmos mandatos aumentaram para 2,00% e 5,72% ao ano. Uma alocação de 5% pode ser sugerida para investidores que aplicam em renda fixa, dado que o retorno continua 100% positivo ao longo do tempo o VAR e teste de stress estimados não apresentam resultados esperados negativo. Uma alocação maior, de até 20% pode melhorar os resultados, porém cabe ao investidor saber seu nível de aversão a perda.

A carteira de renda variável, apesar da carteira encontra-se abaixo da FE sugerida pelo modelo, apresentou benefício de menor volatilidade promovendo também um retorno acumulado maior. O retorno total do portfolio de 920,70% superando o benchmark em 144,21%. O risco decaiu para 19,5% ea volatilidadedownside é de 10,09%. O beta em 0,65 demonstra menor sensibilidade ao risco de mercado, e alfa de 0,09%.

Pode-se concluir que as carteiras que possuíram ouro em sua alocação apresentaram retornos superiores aos benchmarks ao longo da série, e, conforme MPT, a diversificação de ativos pouco correlacionados promoveu a redução de risco, principalmente em comparação a ativos voláteis. O arcabouço da teoria financeira comprova que o investir na commodity no Brasil resultou em agregação de performance as carteiras de fundos de investimento.

Caso tenha lido até o final, agradeço e espero que tenha gostado do conteúdo!

E caso tenha alguma duvida ou queira analisar a tabela com os resultados, estou a disposição para mais informações no e-mail:

guilherme@contratofuturo.com

 

Um grande abraço,

 

– Guilherme Renato Rossler Zanin

 

 

Disclaimer:

Este artigo tem propósitos informativos e didáticos. Nenhuma decisão de investimento deve ser tomada apenas com o exposto no artigo. O presente texto NÃO CONSTITUI RECOMENDAÇÃO OU ACONSELHAMENTO de nenhuma espécie, NÃO projeta, NÃO garante nenhum lucro, NÃO valida nenhuma decisão, tampouco ou autor ou a contratofuturo.com pode ser responsabilizada por eventuais ganhos ou perdas financeiras de quem dela se utilizar.

O presente artigo tem APENAS A INTENÇÃO DE RETRATAR UM MOMENTO ESPECÌFICO DE UM ATIVO DO MERCADO FINANCEIRO e expor, DIDATICAMENTE uma possível estratégia operacional.

Consulte seu operador, principalmente se não souberes interpretar os resultados / utilizar o presente artigo. O operador é a pessoa habilitada a ajudá-lo na tomada de qualquer decisão de investimento e esclarecer os propósitos desse artigo.

Todos os direitos deste artigo são reservados a Guilherme Renato Rossler Zanin e a contratofuturo.com, sendo expressamente proibida a divulgação deste conteúdo sem a solicitação do autor e a fonte contratofuturo.com.