O Efeito Turn of the Month – Evidências Históricas e Empíricas de Sazonalidade no IBovespa

INTRODUÇÃO

 

        Anomalias do mercado financeiro causadas por eventos assimétricos, essencialmente aleatórios, são contradições dos pressupostos da Hipótese de Mercado Eficiente. Este conceito, apresentando pelo prêmio Nobel Eugene Fama (1970), é um dos alicerces dos modelos matemáticos de Finanças, o qual sugere que os investidores não podem antever eventos futuros e assim auferir retornos acima do mercado no longo prazo. Em contraponto, estudos sobre padrões recorrentes como Earnings Suprises, Calendar Effects, P/E Effect, size Effect, dentre outros, evidenciam a persistência de eventos sazonais em series financeiras e que os agentes econômicos podem explorar estas exceções, obtendo assim performance superior.

        Fazendo um paralelo a estes eventos, este artigo objetiva investigar um dos principais efeitos calendário de senso comum em finanças. Existe o Efeito da Virada do Mês (Turn of the Month - ToM) na bolsa de valores brasileira? No intuito de avaliar empiricamente se existe previsibilidade sazonal no primeiro e último dia de cada mês, sendo esta persistente ao longo do tempo, factual e explorável por seus agentes.

         Realizando uma releitura do arcabouço teórico da Hipótese do Mercado Eficiente, é racional supor que a oscilação nos preços dos ativos financeiros segue o modelo de passeio aleatório (random walk model), sendo estes imprevisíveis e independentes dos preços passados. Ademais, os valores correntes destes ativos congregam todas as informações disponíveis que possam afetar as expectativas sobre o retorno futuro, a percepção de risco e liquidez do ativo. Este artigo não tem por objetivo pesquisar e analisar as evidências que comprovem ou discordem desta abordagem. Entretanto, tendo em vista a possibilidade de existência de fatores cíclicos persistentes, é possível refutar a HME caso seja comprovado padrões constante no mercado.

          O presente trabalho objetiva verificar a existência de sazonalidades oriundas da virada de mês, ou seja, foram analisados se os primeiros e os últimos dias do mês apresentam rendimentos superiores ou inferiores aos demais dias do mês. Entre as possíveis explicações para a existência deste efeito está o rebalanceamento das carteiras realizado pelos grandes fundos de investimento, que recebem periodicamente aportes dos quotistas e necessitam redimensionar os portfolios neste período específico para apresentar resultados alinhados com as obrigações dos seus mandatos.

          As análises do efeito Turn of the Month basearam-se em dois vetores: análise estatística histórica, em que será verificado os retornos e a volatilidade do benchmark em comparação à média histórica; análise econométrica, através de modelos da família ARCH. Inicialmente os modelos econométricos não consideravam o fato da volatilidade variar ao longo do tempo, porém Engle (1982) desenvolveu um modelo denominado ARCH (Autoregressive Conditional Heterocedasticity) que considera a variância ser heterocedástica, ou seja, não é constante ao longo do tempo. Posteriormente foram realizadas importantes extensões deste modelo que consideram que a variância condicional é uma função linear do quadrado das inovações passadas, sendo eles a sua versão generalizada proposta por Bollerslev (1986), denominadas GARCH (Generalized Autoregressive Conditional Heterocedasticity) e a versão para períodos cíclicos assimétricos de cauda longa P-GARCH (Periódic Garch).

           Desta forma, o presente artigo é estruturado apresentando na sessão 1 uma revisão bibliográfica sobre os temas acima citados, precedendo os procedimentos metodológicos tanto histórico como econométrico ARCH, GARCH, P-GARCH, os quais serão apresentados na sessão 2. Sendo o arcabouço teórico esclarecido, a sessão 3 analisa os resultados manifestados no principal benchmark do mercado financeiro brasileiro, o IBovespa. Na sessão 4 concluísse se há evidências persistentes do efeito Turn of the Month e se é uma anomalia contradizem-te a HME e explorável pelos seus agentes.

 

REVISÃO DA BIBLIOGRAFIA

 

            Assaf Neto (2013) descreve que contexto de um mercado financeiro eficiente, o valor de um ativo é reflexo do consenso dos participantes com relação ao seu desempenho esperado. Na Hipótese de Mercado Eficiência (HME), o preço de um ativo qualquer é formado com base nas informações públicas disponíveis aos investidores. Um mercado eficiente é entendido como aquele em que os preços refletem as informações disponíveis e apresentam grande sensibilidade aos novos dados, ajustando-se rapidamente a outros cenários. De acordo com Fama (1970) sendo os mercados eficientes não seria possível a obtenção de retornos anômalos, acima de algum índice de referência. Devido à simetria informacional existente, os preços dos ativos seriam alterados rapidamente e incorporado os novos fatos de forma uniforme.

            Sobre o assunto, Damoradan (1996) coloca ainda que a eficiência de mercado não exige que haja sempre uma coincidência entre o preço de um mercado de um ativo e seu valor real. Segundo o autor, as hipóteses básicas do mercado eficiente são:

            Hipótese a: nenhum participante do mercado tem a capacidade de sozinho influenciar os preços negociados, alterando-os segundo exclusivamente suas expectativas;

            Hipótese b: o mercado, de uma maneira geral, é constituído de investidores racionais, decidindo sobre alternativas que promovam o maior retorno possível para determinado nível de risco, ou o menor risco possível para um certo patamar de retorno;

            Hipótese c: todas as informações estão disponíveis aos participantes do mercado, de maneira instantânea e gratuita. Nessa hipótese, nenhum investidor apresenta qualquer acesso privilegiado as informações;

            Hipótese d: a inexistência de racionamento de capital, permitindo que todos os agentes do mercado tenham acesso equivalente às fontes de crédito;

            Hipótese e: os ativos objetos do mercado são perfeitamente divisíveis e negociados sem restrições;

            Hipótese f: as expectativas dos investidores são homogêneas, isto é, apresentam o mesmo nível de apreciação com relação ao desempenho do futuro.

         Dyckman e Morse (1986) sugerem que o mercado acionário apresenta certas características que o tornam mais eficiente que a maioria dos demais mercados. Segundo os autores, a maior eficiência mostrada pelo mercado de ações é determinada, basicamente:

 

• - pela rapidez com que as ordens de compra e venda são executadas dentro do ambiente organizado desses mercados;
• - Pelo elevado número de participantes que se encontram geralmente envolvidos com as ações: investidores individuais e institucionais, corporações, instituições financeiras etc;
• - Pela maior disseminação das informações das empresas, permitindo um ajuste mais rápido dos valores do mercado de ações.

 

        Para completar a HME, Fama (1970) concorda que os mercados financeiros de diversos países não regem as informações no mesmo grau de agilidade e precisão. Devido a este fator, ele divide a HME em uma escala de eficiência em três forma: forte, semifortes e fraca.

         Posteriormente, essas hipóteses de perfeição de comportamento do mercado foram sendo abandonadas, conforme descrito por Fox (2010). Entre os aspectos de imperfeição de mercado pelos quais os modelos financeiros precisam ser testados, podem ser citados:

 

• - Não há homogeneidade nas estimativas dos investidores;
• - Identicamente, o mercado não é composto unicamente de investidores racionais. Existe grupos de participantes que frequentemente comete erros em suas decisões, refletindo sobre o desempenho do todo o mercado;
• - O mercado não é necessariamente sempre eficiente para valorar seus ativos negociados, sofrendo decisivas influencias de políticas econômicas adotadas pelo governo.

         

         Quando evidenciasse um mercado de baixa eficiência, a preocupação principal está em avaliar se os investidores que atuam no mercado conseguem tirar proveito econômico dos desvios temporárias dos preços de certos ativos.

         Estudos relacionados ao mercado financeiro citam que apesar da aleatoriedade dos retornos, random walk conforme descrito por Fama (1970), é possível identificar certos ciclos sazonais em series financeiras. Chamados de “efeitos calendário”, estes padrões são previamente conhecidos tanto em commodities agrícolas como no consumo elétrico e festivo, sendo um componente sazonal recorrente e perceptível pelos agentes econômicos. Conforme descrito na HME, os investidores mais atentos poderiam realizar arbitragem assim que vislumbrarem uma oportunidade (assimetria de mercado), sendo esta anomalia rapidamente explorada, corrigindo o erro gerado. Através desta abordagem poderia se concluir que não haveria a possibilidade de retornos acima do comum no longo prazo derivados dos efeitos calendários.

          Estas anomalias geradas pelo efeito calendário foram estudadas com maior rigor em diversos trabalhos acadêmicos e comprovada estatisticamente como recorrentes, refutando assim a HME. Entre os exemplos de ciclos sazonais estudados estão o dia da semana (Day of the Week Effect) e efeito janeiro (January Effect). Outro evento, o sell in May, é considerado por muitos como uma mera superstição e o estudo de Tinic (1984) não conseguiu comprovar a persistência deste evento.

           O Turn of the Month Effect é um padrão sazonal cíclico conhecido o qual sugere que os retornos dos ativos são superiores nos últimos e primeiros dias do mês. Uma possível explicação para a existência desta oscilação excessiva nestes dias é dada graças ao rebalanceamento de carteiras realizado pelos grandes fundos de investimento, que recebem periodicamente aportes dos quotistas e exercem uma certa pressão compradora ou vendedora neste período específico. Outro ponto relatado por Benjamim Pham (2002) é que o incentivo para realocação de ativos nestes dias é maior devido ao fechamento mensal das cotas, sendo este um fator importante para os gestores quando eles prestam contas para seus cotistas com relação as suas posições. O primeiro e último dia do mês seriam decisivos para os grandes agentes devido ao fato que seus relatórios precisam estar em linha com os seus mandatos, gerando por consequência uma volatilidade nos retornos acima da média no mercado nestes dias.

           Assim como outras anomalias, este efeito sazonal parece estar presente na maioria dos mercados de ação mundial. No artigo de Eleftherios Giovanis (2014) é examinado o efeito ToM em 20 países e este encontra evidências significativas estatisticamente de que ele é persistente em 19 deles, incluindo o Brasil. Já o estudo de Benjamim Pham (2002) também reforça a existência deste efeito no índice americano SP500, assim como Denis O. Boudreaux (1995) comprovou a presença de ToM em 3 dos 7 países da Europa.

          Alguns estudos sobre o mercado brasileiros, como Bampi, Colombo e Barcelos (2009), comprovam que os retornos são superiores no índice Bovespa no último dia do mês e primeiro dia subsequente. Esta oscilação acima da média confirma o comportamento previsível e recorrentes nas séries temporais financeiras locais, sendo assim explorável pelos seus agentes econômicos e contra a HME.

          Neste artigo abordarei o ToM no IBOVESPA em uma janela temporal maior que os autores anteriores e utilizarei dois métodos diferentes, um histórico e outro econométrico em comunhão. Visando comprovar a suposta previsibilidade, relacionada as sazonalidades, é avaliado se o efeito Turn of the Month é recorrente ao longo do tempo no mercado brasileiro.

 

PROCEDIMENTOS METODOLÓGICOS  

 

           Para investigar o efeito Turn of the Month, foi coletada a base histórica do índice Bovespa na plataforma Broadcast AE entre os períodos de janeiro de 03/01/2000 à 22/09/2014, uma série temporal de 3647 pregões. Posteriormente utilizou-se tanto do Excel como do programa Stata para realização dos testes econométricos. Para trabalhar com os dados foi necessária também a realizada a variação logaritmo natural dos retornos do IBovespa, ln(IBovespa), com o objetivo de tornar a série estacionaria, sendo média zero e variância constante nos retornos.

           Para criação das dummys a serem estudadas na série temporal, inicialmente fora separado o primeiro dia do mês (First) dos demais, fixando valor 1 para tal e 0 para os demais. Posteriormente foi criada a segunda dummy relacionada ao último e o primeiro dia de cada mês de pregão, referente ao efeito ToM, fixando valor 1 para tais dias e 0 para os demais.

            Historicamente o principal índice da bolsa de valores brasileira apresenta padrão não estocástico positivo ao longo dos últimos 15 anos, conforme evidenciado gráfico (1).

Índice Bovespa, série histórica

Fonte: Stata – Elaboração do autor

          Os resultados da tabela 1 demonstram que a média do Ibovespa ao longo dos últimos 14 anos foi de 39.695 pontos, tendo o ápice em 73.516 e menor valor de 8.370 pontos após o ano 2000. Os retornos diários no longo prazo são de 0,05021% ao dia, com desvio padrão de 1,84472%.

          A variação dos logarítmica indica que os retornos apresentam clusters de volatilidade alternando entre os anos 2001, 2008 e 2012, todos períodos econômicos de grande relevância histórica.

 

   Variable |       Obs       Mean   Std. Dev.       Min       Max

-------------+--------------------------------------------------------

       ibov |     3647   39695.94   20245.45   8370.88   73516.81

     lnibov |     3647   .0005021   .0184472 -.1139312   .1465784

Fonte: Stata – Elaboração do autor

 

          O gráfico 2, histogram dos retornos, demonstra uma distribuição normal, porém a skewness de 0,57427 indica que a série não é homoscedástica. Alguns retornos anômalos na série, tanto na cauda positiva (0.1465784) como negativa (-0.1139312), além da Kurtosis 7.148164 evidenciam que o ativo é não estocástico em nível.

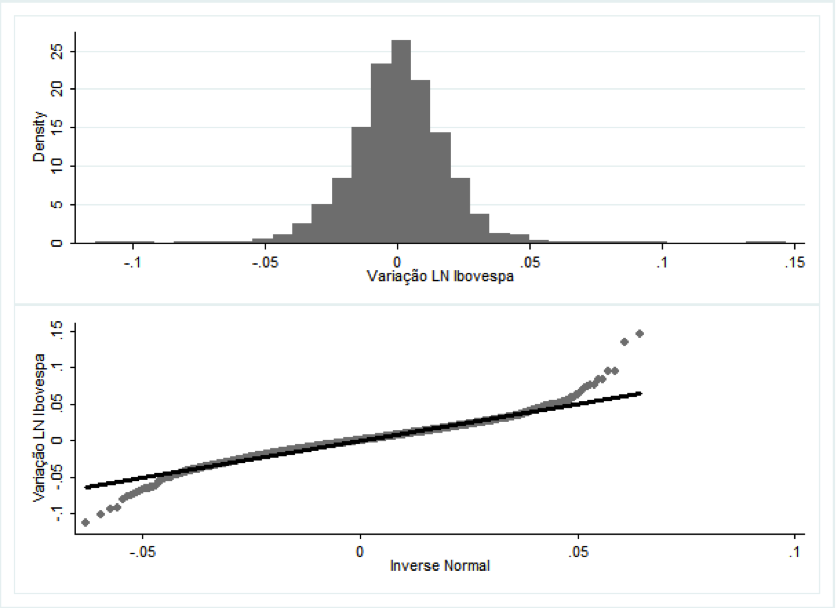
Fonte: Stata – Elaboração do autor

            A diferença de visualizar os dados pelo método histórico e testa-los pelo método econométrico está na robustez dos resultados encontrados. Um estudo empírico resulta estatisticamente em um modelo mais sólido que os métodos tradicionais subjetivos, sendo este um dos alicerces mais importantes para as fundamentações econômicas.

           Os modelos iniciais de econometria não consideravam o fato da volatilidade variar ao longo do tempo. Engle (1982) foi o primeiro a desenvolver um modelo denominado ARCH (Autoregressive Conditional Heterocedasticity) que considera a variância ser heterocedástica, ou seja, não é constante ao longo do tempo. Neste modelo, a variância condicional é uma função linear do quadrado das inovações passadas. Assim sendo, o modelo ARCH (q) pode ser representado da seguinte forma:

(o retorno em t é igual a uma constante acrescida do erro residual do modelo em t),

,       ,

(informações disponíveis em t-1),

,

Para esse modelo ser bem definido e a variância condicional ser positiva, as restrições paramétricas devem satisfazer  e > 0,   i = 1,2,.......,p

          Uma importante extensão do modelo ARCH é a sua versão generalizada proposta por Bollerslev (1986), denominada GARCH (Generalized Autoregressive Conditional Heterocedasticity). Neste modelo, a função linear da variância condicional inclui também variâncias passadas. Assim sendo, a volatilidade dos retornos depende dos quadrados dos erros anteriores e também de sua própria variância em momentos anteriores. A variância é dada da seguinte forma:

onde as restrições são dadas por: >0, i = 1,2,.....q ; b > 0 , j = 1,2,....,p e . Assim sendo, segue um modelo GARCH (p,q), onde q representa a ordem do componente ARCH e p a ordem do componente GARCH.

            Bueno (2011) apresenta uma variação do GARCH que busca captar uma assimetria potencial especifica a um determinado ciclo. O modelo PARCH, proposto inicialmente por Ding, Granger e Engle (1993), é a variação do GARCH que captura um processo de memória longa, por meio da liberdade dada ao coeficiente e ênfase ao ciclo .

onde as restrições são dadas por: , for , e , e . O

O ponto interessante deste modelo que ele captura a assimetria por meio do parâmetro , o qual é fixado = 0 e = 1. Sendo esta imposição fixada anteriormente nas variáveis dummys ToM e First, foi possível restringir os ciclos desejados e avalia-los separadamente.

 

RESULTADOS

 

            Os resultados encontrados, tanto pelo método histórico como pelo método econométrico não divergem das evidências apresentadas pelos outros estudos referentes a persistência do efeito Turn of the Month no mercado brasileiro.

           Pelo método histórico, após tabula-los separadamente conforme gráfico 2, os retornos do primeiro e último dia de cada mês não apresentam padrão determinístico.

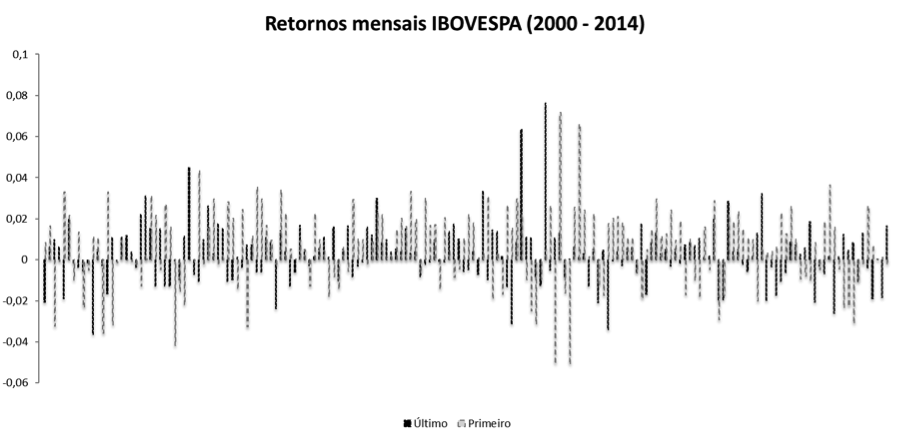
Fonte: Excel – Elaboração do autor

                

           A média da volatilidade do último dia no mês, durante 176 pregões, foi de 0,27%, sendo assim superior à média dos outros dias (0,01%) em que não constam os clusters. Já o a volatilidade do primeiro dia do mês foi em média de 0,59%, sendo o maior dia de toda a série. Este resultado indica que existem evidências históricas que comprovam que o primeiro dia do mês é mais volátil que os demais dias, sendo comprovado o efeito ToM. Quando adicionado o primeiro e último dia do mês aos demais, eles aumentam a volatilidade da média da série de retornos de todos os dias para 0,05%.

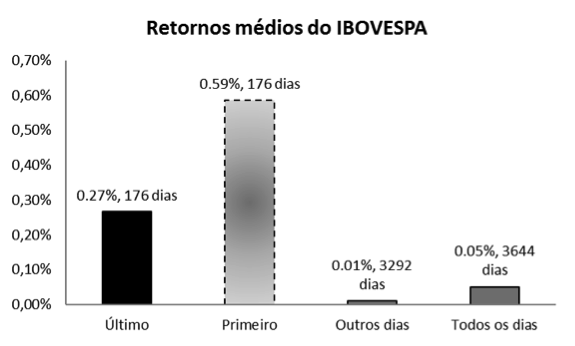
            O menor resultado no último dia do mês foi de -3,63% e o maior de 7,63%. Sendo a soma dos resultados em 46,80%, as evidências indicam que a assimetria dos retornos é positiva. Em consonância com os resultados anteriores, o primeiro dia do mês apresenta retorno máximo de 7,17% e mínimo de -5,10%, tendo a soma dos retornos em 103,07%, uma assimetria positiva maior que o último dia do mês e também maior que a soma dos demais.

 

 

            Com as evidências históricas da persistência do efeito ToM, os dias foram separados em positivos ou negativo. Os resultados mostram que em 59,09% dos pregões do IBovespa o mercado apresenta resultados positivos no último dia do mês e 63,64% nos primeiros dias do mês.

 

         Apesar das demonstrações históricas deixarem clara volatilidade e a assimetria positiva durante o Turn of the Month, estatisticamente não pode-se comprovar a veracidade dos resultados. Para tal comprovação precisa utilizar um método econométrico, porém, inicialmente precisasse cumprir alguns pré-requisitos para garantir a estimação e previsão da série com significância estatística nos resultados.

        Para estimação de serieis financeiras onde a volatilidade é um fator chave, seu tratamento tem de ser diferenciado dos modelos clássicos de series temporais ARMA (Autoregressive Moving Average) segundo Bueno (2011), pois estes não reproduzem alguns fatos utilizados, como a não normalidade condicional/incondicional e a variância condicional não constante ao longo do tempo. Além do mais, ARMAs e ARIMAs modelam apenas em nível e não sua variância.

         Avaliando primeiro o índice Bovespa em nível, através do teste Dickey-Fuller de raiz unitária, é verificado se a série é estacionaria estatisticamente. O índice demonstrou que a série é não estacionarias em com 90% de significância, p-valor de 10%.

 

Dickey-Fuller test for unit root                   Number of obs   =     3645

                               ---------- Interpolated Dickey-Fuller ---------

                 Test         1% Critical       5% Critical     10% Critical

               Statistic           Value             Value             Value

------------------------------------------------------------------------------

Z(t)             -1.221           -3.430           -2.860           -2.570

------------------------------------------------------------------------------

MacKinnon approximate p-value for Z(t) = 0.6645

 

          Para correção do problema de raiz unitária, a modelagem de séries estacionarias em diferença lognatural pode ser implementada, de acordo com a abordagem de Box e Jankins (Bueno 2011). Segundo o autor, uma série não-estacionaria pode ser transformada em estacionaria utilizando-se usualmente a primeira diferença dos retornos. O resultado do teste DF do Ln Ibovespa indica que a série é estacionaria em 99% .

 

Dickey-Fuller test for unit root                   Number of obs   =     3645

 

                              ---------- Interpolated Dickey-Fuller ---------

                 Test         1% Critical       5% Critical     10% Critical

               Statistic           Value             Value             Value

------------------------------------------------------------------------------

Z(t)           -60.076           -3.430           -2.860           -2.570

------------------------------------------------------------------------------

MacKinnon approximate p-value for Z(t) = 0.0000

 

           Um dos modos estudados em econometria para analisar qual é a o impacto das variáveis em um modelo é através do método de regressão múltiplas das variáveis dummys. Apresentando a regressão do Ln Ibov, é possível verificar se existe relação significativa entre os retornos. Primeiro verificasse se há problema heteroscestidcidade proveniente da variância dos erros da serie através do teste de Breusch-Pagan LM sugerido por Bueno (2011), pela formula:

em que

          Como o teste LM mostra um valor de P>c de 0,00, estando abaixo de 0,05, rejeita-se a hipótese nula de inexistência de efeitos ARCH (1), sendo a série heteroscedastica.

 

LM test for autoregressive conditional heteroskedasticity (ARCH)

---------------------------------------------------------------------------

   lags(p) |         chi2               df                 Prob > chi2

-------------+-------------------------------------------------------------

       1     |         78.013              1                   0.0000

---------------------------------------------------------------------------

         H0: no ARCH effects     vs. H1: ARCH(p) disturbance

 

           Sendo a série estacionaria e corrigido o problema de heteroscedasticidade da série com o problema Robust, a regressão das variáveis ToM e First day pelo índice Bovespa evidenciam a assimetria positiva do evento Turn of the Month com significância de 95% (p>t 0,034) e First day de 90% (p>t 0,072), sendo os eventos calendários comprovados estatisticamente. Apesar de grande parte da literatura acadêmica sugerir que 95% e 99% são as convenções mais comuns para estes testes, a evidências empíricas indicam que estes dias apresentam retornos positivos e são comprovados no mercado brasileiro.

 

Linear regression                                     Number of obs =   3647

                                                       F( 2, 3644) =   9.10

                                                      Prob > F     = 0.0001

                                                       R-squared     = 0.0051

                                                       Root MSE     = .01841

------------------------------------------------------------------------------

             |               Robust

     lnibov |     Coef.   Std. Err.     t   P>|t|     [95% Conf. Interval]

-------------+----------------------------------------------------------------

         tom |   .0024443   .001153     2.12   0.034     .0001838   .0047048

       first |   .0033053   .0018395     1.80   0.072   -.0003013   .0069119

       _cons |   .000106   .0003227     0.33   0.743   -.0005267   .0007388

 

            Comprovada que heteroscedasticidade da série, buscasse avaliar se a variância condicional das dummys é superior aos demais dias através de modelos de volatilidade implícita. Sendo a variância condicional aos eventos passados, os modelos da família ARCH de Engle (1982) buscam captar a assimetria dos retornos comparados ao efeito ToM e First. Inicialmente foi realizado o teste via modelo ARCH(1) em nível, de distribuição T-student e variância heteroscedastica.

 

ARCH family regression -- multiplicative heteroskedasticity

Sample: 03/01/2000 to 22/09/2014, but with a gap Number of obs   =     3647

Distribution: t                                   Wald chi2(.)   =         .

Log likelihood = 9599.576                         Prob > chi2     =         .

------------------------------------------------------------------------------

             |                 OPG

     lnibov |     Coef.   Std. Err.     z   P>|z|     [95% Conf. Interval]

-------------+----------------------------------------------------------------

lnibov       |

       _cons |   .0007725   .0002694     2.87   0.004     .0002445   .0013004

-------------+----------------------------------------------------------------

HET         |

         tom | -.6311236   .1545974   -4.08   0.000   -.9341289   -.3281182

       first |   1.098194   .2184631     5.03   0.000     .6700147   1.526374

       _cons | -8.150135   .0440183 -185.15   0.000     -8.23641   -8.063861

-------------+----------------------------------------------------------------

ARCH         |

       arch |

         L1. |   .131137   .0236163     5.55   0.000     .0848498   .1774241

-------------+----------------------------------------------------------------

     /lndfm2 |   1.327769   .1372578     9.67   0.000     1.058749     1.59679

-------------+----------------------------------------------------------------

         df |   5.772619   .5178213                     4.882763   6.937158

 

            O modelo inicial comprova a existência de efeito ARCH na série financeira, em consonância com o teste Breusch-Pagan. A segunda evidência empírica encontrada é que a constante dos log retornos é positiva, sendo o mercado assimétricos. Por fim, tanto o efeito ToM e First são econometricamente comprovados, sendo assim seus retornos das dummys superiores à média do mercado.

           O modelo ARCH generalizado de primeira ordem GARCH (Bollerslev 1986) é a especificação mais comumente usada para a variância condicional em trabalhos empíricos e geralmente denotado como GARCH(1, 1). Pode-se estimar um processo GARCH(1, 1) para a série de logaritmos diferenciados, dando mais liberdade para avaliar os impactos dos efeitos calendários sobre a série completa. Sendo a série estacionarias um dos pré-requisitos, segundo Bueno (2011), foi realizado um teste via modelo GARCH(1) em variação logarítmica e variância heteroscedastica das dummys ToM e First day.

 

ARCH family regression -- multiplicative heteroskedasticity

Sample: 03/01/2000 to 22/09/2014, but with a gap  Number of obs   =     3647

Distribution: Gaussian                             Wald chi2(.)   =         .

Log likelihood =   9747.11                         Prob > chi2     =         .

------------------------------------------------------------------------------

             |                OPG

     lnibov |     Coef.   Std. Err.     z   P>|z|     [95% Conf. Interval]

-------------+----------------------------------------------------------------

lnibov       |

       _cons |   .0007065   .0002609     2.71   0.007     .0001951   .0012179

-------------+----------------------------------------------------------------

HET         |

         tom | -23.49442   .6548445   -35.88   0.000   -24.77789   -22.21095

       first |   27.05434         .       .       .           .           .

       _cons |   -13.0152   .558586   -23.30   0.000   -14.11001   -11.92039

-------------+----------------------------------------------------------------

ARCH         |

       arch |

         L1. |   .0688565   .0064609   10.66   0.000     .0561934   .0815196

             |

       garch |

         L1. |   .9127171   .0081535   111.94   0.000     .8967366   .9286976

------------------------------------------------------------------------------

 

            O modelo GARCH comprova ser adequado estatisticamente, além de ser adequado a série do Ibovespa. A constante é menor que o modelo ARCH apresentado inicialmente, porém ainda dentro do intervalo de confiança. O resultado do efeito ToM também rejeita a hipótese anula, aceitando a hipótese alternativa de que ele é positivo e comprovado estatisticamente.

            Vista a assimetria dos retornos inerente ao mercado financeiro, principalmente relacionada a eventos anômalos na economia, um modelo que captura essa característica dos resultados de cauda longa, sugerido por Moretin (2009), é o PGARCH (Periódic Garch). Novamente, sendo a série não-estacionarias um dos pré-requisitos, Bueno (2011), foi realizado um teste via modelo PGARCH(1) em variação logarítmica e variância heteroscedastica das dummys ToM e First day.

 

ARCH family regression -- multiplicative heteroskedasticity

Sample: 03/01/2000 to 22/09/2014, but with a gap  Number of obs   =     3647

Distribution: Gaussian                             Wald chi2(.)   =        .

Log likelihood =   9747.18                         Prob > chi2     =         .

------------------------------------------------------------------------------

             |                 OPG

     lnibov |     Coef.   Std. Err.     z   P>|z|    [95% Conf. Interval]

-------------+----------------------------------------------------------------

lnibov       |

       _cons |   .0007096   .000261     2.72   0.007     .000198   .0012212

-------------+----------------------------------------------------------------

HET         |

         tom | -35.94062   .8744699   -41.10   0.000   -37.65455   -34.22669

       first |   39.1381         .       .       .           .           .

       _cons | -12.64965   .8231583   -15.37   0.000   -14.26301   -11.03629

-------------+----------------------------------------------------------------

ARCH         |

     pgarch |

         L1. |   2.037865   .0634118   32.14   0.000     1.91358     2.16215

       arch |

         L1. |   .0676843   .007322     9.24   0.000     .0533335   .0820351

       garch |

         L1. | -1.100935         .       .       .           .           .

-------------+----------------------------------------------------------------

POWER       |

       power |   2.006376   .0160521   124.99   0.000     1.974914   2.037838

------------------------------------------------------------------------------

 

        Os resultados do modelo PGARCH também sugerem que o efeito ToM é comprovado no mercado, sendo significante estatisticamente.

        Tabulando todos os resultados, Bueno (2011) sugere que o modelo mais adequado para modelar a série do Ibovespa é resultante do menor valor encontrado pela estatística AIC e BIC. Apesar das semelhanças dos modelos, visto que são derivados das estimações de variância condicional, os resultados sugerem que o modelo GARCH é o mais adequado para modelar a série, ajustando os preços e a volatilidade implícita encontrada de forma mais adequada.

 

. estimates table ARCH GARCH PGARCH, stats(aic bic)

-----------------------------------------------------

   Variable |   ARCH       GARCH       PGARCH  

-------------+---------------------------------------

lnibov       |

       _cons | .00077248     .0007065   .00070961

-------------+---------------------------------------

HET         |

         tom | -.63112356   -23.494421   -35.940621

       first | 1.0981944   27.054342   39.138097

       _cons | -8.1501354     -13.0152   -12.649649

-------------+---------------------------------------

ARCH         |

       arch |

         L1. | .13113697   .06885646   .06768429

             |

       garch |

         L1. |               .91271708   -1.1009353

             |

     pgarch |

         L1. |                           2.0378653

-------------+---------------------------------------

lndfm2       |

       _cons | 1.3277695                          

-------------+---------------------------------------

POWER       |

       power |                             2.006376

-------------+---------------------------------------

Statistics   |                                      

         aic | -19187.152   -19484.219   -19482.361

         bic | -19149.942   -19453.211   -19445.151

-----------------------------------------------------

        Todos os resultados estimados dos modelos ARCH entram em consonância com a teoria financeira de que os retornos dos eventos ToM e First são anômalos, aceitando a hipótese de eventos sazonais são recorrentes durante estes dias específicos.

 

CONSIDERAÇÕES FINAIS

 

        Concluindo, os resultados preliminares sugerem que o efeito Turn of the Month é presente e forte no mercado brasileiro, em linha com estudos acadêmicos encontrados sobre o assunto. Apesar da Hipótese do Mercado Eficiente indicar que os retornos de séries financeiras são essencialmente aleatórios (random walk), as evidências empíricas apresentadas neste artigo diferem desta hipótese, sugerindo que os eventos calendários, relacionados a sazonalidade, são recorrentes e previsíveis ao longo do tempo.

       No presente artigo foram apresentadas duas metodologias que evidenciam a volatilidade anormal do mercado nos primeiros e últimos dias na bolsa de valores local. O resultado histórico sugere que a volatilidade dos retornos no Ibovespa é positiva para estes dias, sendo superior a 60% e assimetricamente positiva. Sendo assim, o histórico do mercado comprova que os primeiros e últimos dias do mês são mais voláteis que os demais dias, sendo assim presente o efeito ToM.

       Os resultados das análises econométricas indicam que a série de pontos índice é estocástica e que os modelos heteroscedásticos da familia ARCH são os mais apropriados para avaliação da análise dos retornos anômalos de volatilidade. O modelo para serieis assimétricas que captura resultados da cauda longa PGACH não apresenta resultados muito diferentes do modelo generalizado GARCH proposto por Bollerslev (1986), sendo este o mais adequado para modelar a série. Todos os resultados comprovaram a existe de evidências do efeito ToM e First estatisticamente.

       Dada a skewness positiva da volatilidade implícita maior durante the First day e o efeito ToM comparada aos demais dias do mês, este artigo pode concluir que existem evidências empíricas que indicam a existência do efeito de virada do mês. Sendo esta evidente, pode-se refutar a HME forte no mercado brasileiro e que estes eventos calendários pode ser explorado pelos agentes do mercado financeiro.   

       Este estudo poderia agregar diferentes modelos de serieis temporais e apresentar resultados diferentes caso fosse analisados períodos mais longos, porém devido à restrição imposta neste artigo ao mercado financeiro brasileiro e incipiência do mercado em número de benchmarks existentes, limitou o processo de coleta de dados e análise. Para trabalhos futuros a sugestão é analisar os ativos que compõem o Ibovespa separadamente e também avaliar os resultados no mercado internacionais, como os outros estudos apresentados no escopo deste artigo realizaram, a fim de comparar os resultados e comprovar a existência de retornos anômalos provenientes de efeitos calendários.

 

 

 

 

REFERÊNCIAS BIBLIOGRÁFICAS

Ariel, Robert A., “A Monthly Effect in Stock Returns,” Journal of Financial Economics, Vol. 18, pp. 161-174, 1987.

Bollerslev, T., “Generalized Autoregressive Conditional Heterocedasticity” , Journal of Econometrics, 31, 307-327, 1986.

Bueno, Rodrigo de Losso da Silva – Econometria de Séries Temporais. 2 ed. São Paulo, 2011. 

COSTA Jr, N.C.A., Sazonalidades do Ibovespa. Revista de Administração de Empresas, São Paulo, p.79-84, 1990.

Damodaran Aswath, Valuation Approaches and Metrics: A Survey of the Theory and Evidence Aswath Damodaran Stern School of Business November 2006. Link: http://people.stern.nyu.edu/adamodar/pdfiles/papers/valuesurvey.pdf

Denis O. Boudreaux, THE MONTHLY EFFECT IN INTERNATIONAL STOCK MARKETS: EVIDENCE AND IMPLICATION, www.studyfinance.com/jfsd/pdffiles/v8n1/boudreau.pdf

Dr. Nickel (Alexandre Rubens), O Efeito da Virada do Mês e como Explora-lo, link:

https://drnickel.wordpress.com/2014/10/06/o-efeito-da-virada-do-mes-e-como-explora-lo/ 

DYCKMAN, 1. & MORSE, D. Efficient capital markets and accounting, Englewood Cliffs, PrenticeHall, 1986

Engle, R. F., “Autoregressive Conditional Heterocedasticity with Estimates of the Variance of United Kingdom Inflation”. Econometrica, 50, 987-1008.

FAMA, E.F. Eficient capital markets: a review of theory and empirical work. Journal of Finance, v. 25, p. 383417, 1970 (1982). 

FAMA, E.F Random Walks in Stock Price, Financial Analysts Journal (set/1965, republicado em jan-fev/1955), p.76

Stephen D. Simpson, Trading with Market anomalies, http://www.investopedia.com/articles/financial-theory/11/trading-with-market-anomalies.asp#ixzz4fIRuSCqF

FOX, Justin, O Mito dos Mercados Racionais: Uma história de risco, recompensa e decepção em Wall Street. Tradução: Gabriel Zide Neto. Rio de Janeiro: BestSeller, 2010.

Giovanis, Eleftherios, The Turn-of-The-Month-Effect: Evidence from Periodic Generalized Autoregressive Conditional Heteroskedasticity (PGARCH) Model (August 12, 2014). International Journal of Economic Sciences and Applied Research, 7(3), Forthcoming. Link: SSRN: https://ssrn.com/abstract=2479295

NETO, A. A. Mercado Financeiro. 7. ed. São Paulo: Editora Atlas, 2006. NETO, A. A. Mercado Financeiro. 7. ed. São Paulo: Editora Atlas, 2006. NETO, A. A. Mercado Financeiro. 7. ed. São Paulo: Editora Atlas, 2006.

NETO, Alexandre Assaf. Finanças Corporativas e Valor. 6 ed. São Paulo: Ed. Atlas, 2013.

Rodrigo Eduardo Bampi, Jefferson Augusto Colombo, Paulo Fernando Pinto Barcellos, Sazonalidades no Mercado de Capitais: Rendimentos Anormais Relacionados a Eventos do Calendário nas Bolsas de Valores Brasileira e Norte-Americano, www.ingepro.com.br/Publ_2010/Fev/191-547-1-PB.pdf

SILVA, W.V.; FIGUEIREDO, J.N.; SOUZA, A.M. Avaliação do Efeito Dia da Semana nos Retornos dos Índices Bovespa (Brasil), Merval (Argentina) e Dow Jones (Estados Unidos). Anais do XXII Encontro Nacional de Engenharia de Produção. Curitiba, 2002.

Smirlock, Michael, and Laura Starks, “Day of the Week and Intraday Effects in Stock Returns,” Journal of Financial Economics, Vol. 17, 1986, pp. 197-210.

Tinic, Seha M., and Richard R. West, “Risk and Return: January and the Rest of the Year,” Journal of Financial Economics, Vol. 13, December 1984, pp. 561-574.

TORRES, R.; BONOMO, M.; FERNANDO, C. A Aleatoriedade do Passeio na Bovespa: Testando a Eficiência do Mercado Acionário Brasileiro. RBE, Rio de Janeiro, abr-jun. 2002. p.199-247.